数值分析(西安科技大学) 知到智慧树答案2024 z28384
第一章 单元测试
1、 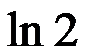 =0.69314718…,精确到10-3的近似值是( )。
=0.69314718…,精确到10-3的近似值是( )。
A:0.700
B:0.69
C:0.6931
D:0.693
答案: 0.693
2、 在下列四个数中,有一个数具有4位有效数字,且其绝对误差限为 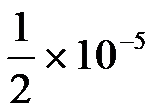 ,则该数是( )
,则该数是( )
A:0.15230
B:0.01523
C:0.001523
D:1.52300
答案: 0.01523
3、 设某数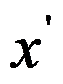 ,对其进行四舍五入的近似值是( ),则它有3位有效数字,绝对误差限是
,对其进行四舍五入的近似值是( ),则它有3位有效数字,绝对误差限是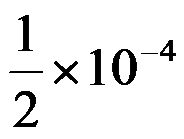 。
。
A:0.0315
B:0.315
C:0.03150
D:0.00315
答案: 0.0315
4、 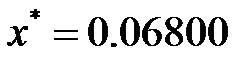 是按“四舍五入”原则得到的近似数,则它有( )位有效数字。
是按“四舍五入”原则得到的近似数,则它有( )位有效数字。
A:2
B:5
C:3
D:4
答案: 4
5、 已知准确值x与其有t位有效数字的近似值x=0.0a1a2…an×10s(a10)的绝对误差x-x( ).
A:0.5×10s+1-t
B:0.5×10 s-t
C:0.5×10 s+t
D:0.5×10 s-1-t
答案: 0.5×10 s-1-t
第二章 单元测试
1、 用二分法求方程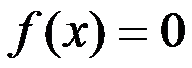 在区间
在区间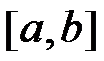 内的根
内的根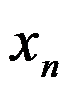 ,已知误差限
,已知误差限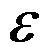 ,确定二分的次数
,确定二分的次数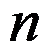 是使( )成立。
是使( )成立。
A: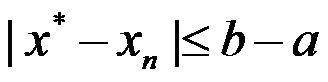
B: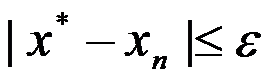
C: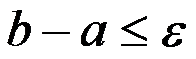
D: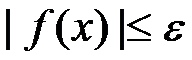
答案: 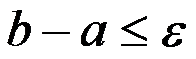
2、 若迭代公式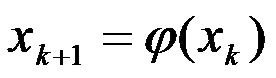 是p阶收敛,则
是p阶收敛,则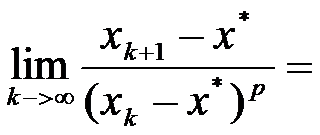 ( )。
( )。
A:0
B: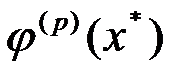
C:p!
D: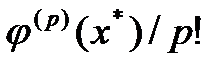
答案: 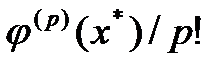
3、 用二分法求解非线性方程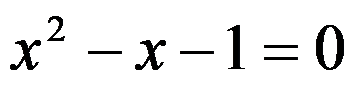 的正根,在初始区间是[0,2]的情况下,若要求误差小于0.05,那么需要二分( )次即可满足要求。
的正根,在初始区间是[0,2]的情况下,若要求误差小于0.05,那么需要二分( )次即可满足要求。
A:3
B:5
C:6
D:4
答案: 5
4、 若已知迭代过程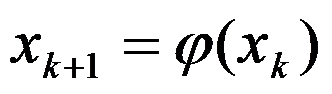 是3阶收敛, C是不为零的常数,则下列式子中,正确的式子是( )。
是3阶收敛, C是不为零的常数,则下列式子中,正确的式子是( )。
A: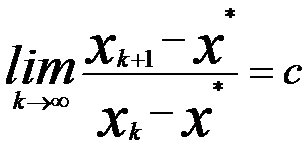
B: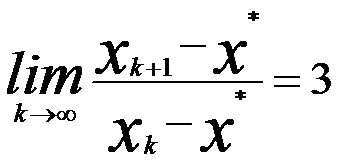
C: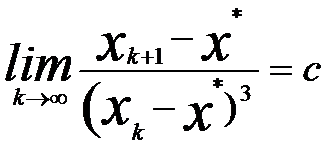
D: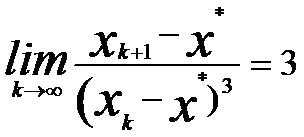
答案: 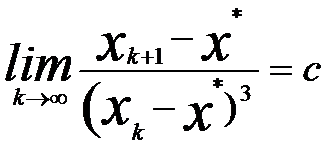
5、 对于迭代过程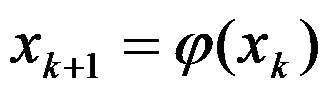 ,如果迭代函数
,如果迭代函数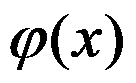 在所求的根
在所求的根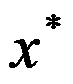 的附近有连续的二阶导数,且
的附近有连续的二阶导数,且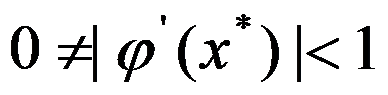 ,则迭代过程( )。
,则迭代过程( )。
A:发散
B:二阶收敛
C:一阶收敛
D:三阶收敛
答案: 一阶收敛
第三章 单元测试
1、
设有迭代公式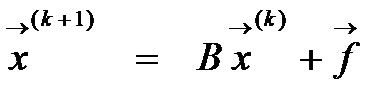 。若||B|| > 1,则该迭代公式( )
。若||B|| > 1,则该迭代公式( )
A:必收敛
B:这三种结果都不是
C:必发散
D:可能收敛也可能发散
答案: 可能收敛也可能发散
2、
设有迭代公式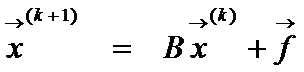 ,则||B|| < 1 是该迭代公式收敛的( )。
,则||B|| < 1 是该迭代公式收敛的( )。
A:必要条件
B:充分条件
C:这三种结果都不是
D:充分必要条件
答案: 充分条件
3、 若行列式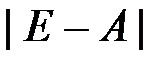 =0,其中
=0,其中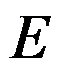 是n阶单位阵,A是n阶方阵,则A的范数满足( )。
是n阶单位阵,A是n阶方阵,则A的范数满足( )。
A: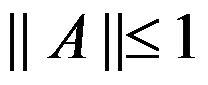
B: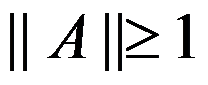
C: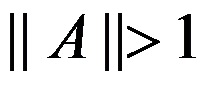
D: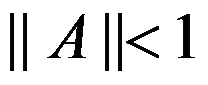
答案: 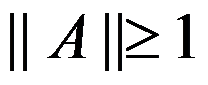
4、 设n阶方阵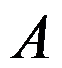 及单位阵
及单位阵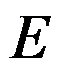 满足
满足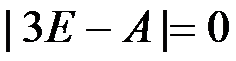 ,则谱半径
,则谱半径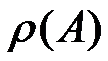 ( )。
( )。
A: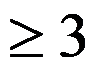
B:<3
C: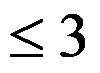
D:>3
答案: 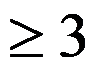
5、 若线性代数方程组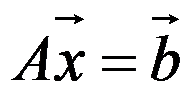 的系数矩阵
的系数矩阵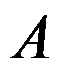 为严格对角占优阵,则雅可比迭代和高斯-塞德尔迭代( )。
为严格对角占优阵,则雅可比迭代和高斯-塞德尔迭代( )。
A:前者收敛,后者发散
B:都收敛
C:都发散
D:前者发散,后者收敛
答案: 都收敛
第四章 单元测试
1、 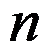 阶方阵
阶方阵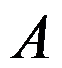 可作
可作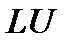 分解的一个充分条件是
分解的一个充分条件是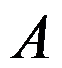 为 ( )。
为 ( )。
A:非奇异阵
B:对角占优阵
C:对称正定阵
D:正交阵
答案: 非奇异阵
2、 设A是n阶方阵,则 A可作唯一LU分解的充分必要条件是( )。
A:A为正交阵
B:A为对角占优阵
C: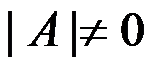
D:A为对称正定阵
答案: 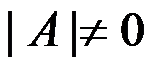
3、 条件数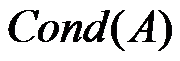 =( )。
=( )。
A: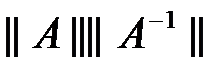
B: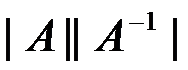
C: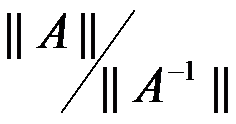
D: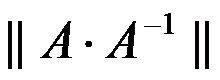
答案: 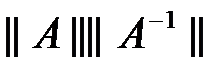
4、 设方阵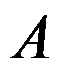 可逆,
可逆,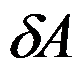 为
为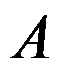 的扰动矩阵,当( )时方阵
的扰动矩阵,当( )时方阵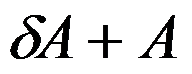 也可逆。
也可逆。
A: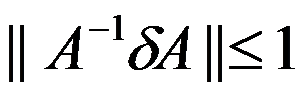
B: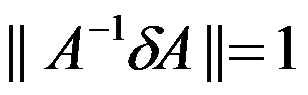
C: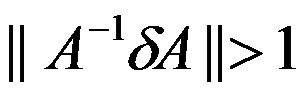
D: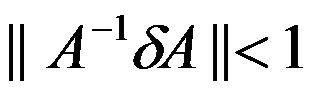
答案: 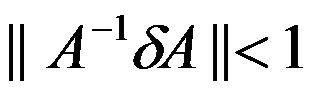
5、 专用来求解三对角形线性方程组的方法是( )
A:雅可比迭代法
B:追赶法
C:LU分解法
D:平方根法
答案: 追赶法
下方是付费阅读内容:本平台商品均为虚拟商品,无法用作二次销售,不支持退换货,请在购买前确认您需要购买的资料准确无误后再购买,望知悉!
完整答案需点击上方按钮支付5元购买,所有答案均为章节测试答案,无期末答案。购买后上方矩形框将出现已付费的隐藏内容。
点关注,不迷路,微信扫一扫下方二维码
关注我们的公众号:阿布查查 随时查看答案,网课轻松过

为了方便下次阅读,建议在浏览器添加书签收藏本网页
电脑浏览器添加/查看书签方法
1.按键盘的ctrl键+D键,收藏本页面

2.下次如何查看收藏的网页?
点击浏览器右上角-【工具】或者【收藏夹】查看收藏的网页

手机浏览器添加/查看书签方法
一、百度APP添加/查看书签方法
1.点击底部五角星收藏本网页

2.下次如何查看收藏的网页?
点击右上角【┇】-再点击【收藏中心】查看

二、其他手机浏览器添加/查看书签方法
1.点击【设置】-【添加书签】收藏本网页

2.下次如何查看收藏的网页?
点击【设置】-【书签/历史】查看收藏的网页

